||🏠
||Чемпионат Урала
||Четвертьфинал ICPC
||УрКОП
||Все соревнования
||Фото
||История
||Новичкам ||
Задачи
Задача X. (Пробный тур) Проба пера
Все что надо - сложить два числа.
Ввод.
Входной файл для этой задачи состоит из двух строк, в каждой из которых записано целое число, лежащее в диапазоне от -32768 до 32767 включительно.
Вывод.
В выходной файл следует записать единственное целое число - сумму двух введенных чисел.
Пример файла input.txt.
150 -34
Пример файла output.txt.
116
Основной тур
Задача A. Ниточка
А.Петров, Н.Шамгунов Злоумышленники варварски вбили в ни в чем не повинную плоскую поверхность N гвоздей, да так, что только шляпки остались. Мало того, они в своих подлых целях вбили все гвозди в вершины выпуклого многоугольника. После этого они... страшно сказать... они натянули ниточку вокруг всех гвоздей, так, что поверхности стало совсем грустно! Вот как примерно они это сделали:
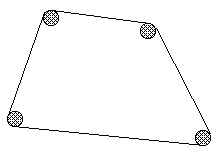
Ввод. В первой строке входного файла к этой задаче находятся два числа - количество гвоздей N, 1 <= N <= 100, и вещественное число R - радиус шляпок гвоздей. Все шляпки имеют одинаковый радиус. Далее во входном файле располагаются еще N строк, в каждой из которых записана через пробел пара вещественных координат центра очередного гвоздя; координаты не превосходят по абсолютной величине числа 100. Описания гвоздей приводятся в порядке обхода вершин многоугольника по или против часовой стрелки, начиная с произвольного гвоздя. Шляпки разных гвоздей не соприкасаются.
Вывод. Выходной файл должен в своей единственной строке содержать вещественное число, округленное до двух знаков после запятой - длину ниточки, натянутой вокруг всех гвоздей.
Пример файла input.txt.
4 1 0.0 0.0 2.0 0.0 2.0 2.0 0.0 2.0Пример файла output.txt.
14.28Задача B. Таинство суммы
Л.Волков, А.Петров
- Брат мой, Магистр Ордена хочет узнать завтра о результатах наших многолетних изысканий. Он хочет видеть, ни много, ни мало, Суммирующую Машину! Даже более того: он хочет, чтобы наша Машина - всего лишь машина - продемонстрировала свое постижение Таинства Суммы настолько глубоко, насколько это возможно. Он хочет, чтобы Машина нашла каких-нибудь два числа, дающих в сумме священное число 10000.
- Тс-с-с! Но это же безумство, граничащее с кощунством! Как Машина может ВЫЧИСЛИТЬ священное число? Двадцать семь лет мы работаем над ней, и смогли только лишь научить ее отвечать на вопрос: "Больше сумма двух введенных чисел, чем 10000, или меньше?". Но разве может смертный найти два таких числа, чтобы их сумма оказалась равна 10000?
- И все же нам придется сделать это с помощью нашей Машины, пусть она и неспособна на это. Иначе у нас будут: ну, скажем так, крупные неприятности, если кипящее масло можно назвать таким словом. Впрочем, у меня есть идея. Помнишь, на той неделе мы ввели в Машину числа -7 и 13, она ответила, что их Сумма меньше 10000. Я не знаю, как это проверить, но нам ничего не остается, как доверять созданию наших рук. Что, если теперь мы возьмем число большее, чем -7 и снова запустим Машину? И будем так делать снова и снова, пока не найдем такое число, которое в сумме с 13 даст 10000. Надо только подготовить список возрастающих чисел.
- Не верю я в эту идею: Давай лучше начнем с суммы, заведомо большей, чем Священное число и будем уменьшать одно из слагаемых, так у нас больше шансов избегнуть кипяще: крупных неприятностей.
Так ни о чем и не договорившись, Братья разошлись по своим кельям. К следующему дню, каждый из них подготовил такой список чисел, который, по его мнению, мог бы их спасти: Смогут ли спасти их оба списка вместе?
Ваша программа должна определять, можно ли из двух списков целых чисел выбрать по одному числу так, чтобы в сумме они составили 10000.
Ввод. В этой задаче есть два входных файла, input1.txt и input2.txt. Формат каждого из этих файлов таков: в первой строчке записано количество Ni чисел в i-том списке, далее в Ni строчках по одному числу в строке записаны сами списки. Выполняются неравенства 1 <= Ni <= 50000, все элементы списков лежат в диапазоне от -32768 до 32767. Первый список упорядочен по возрастанию, второй - по убыванию.
Вывод. В выходной файл следует записать YES, если из списков можно выбрать по числу, которые в сумме дадут 10000 и NO в противном случае.
Пример файла input1.txt.
4 -175 19 19 10424Пример файла input2.txt.
3 8951 -424 -788Пример файла output.txt.
YESЗадача C. Генеалогическое дерево
фольклор, Л.Волков
Система родственных отношений у марсиан достаточно запутана. Собственно говоря, марсиане почкуются когда им угодно и как им угодно, собираясь для этого разными группами, так что у марсианина может быть и один родитель, и несколько десятков, а сотней детей сложно кого-нибудь удивить. Марсиане привыкли к этому, и такой жизненный уклад кажется им естественным.
А вот в Планетарном Совете запутанная генеалогическая система создает серьезные неудобства. Там заседают достойнейшие из марсиан, и поэтому, чтобы никого не обидеть, во всех обсуждениях слово принято предоставлять по очереди, так, чтобы сначала высказывались представители старших поколений, потом те, что помладше, и лишь затем уже самые юные и бездетные марсиане. Однако соблюдение такого порядка на деле представляет собой совсем не простую задачу. Не всегда марсианин знает всех своих родителей, что уж тут говорить про бабушек и дедушек! Но когда по ошибке сначала высказывается праправнук, а потом только молодо выглядящий прапрадед - это настоящий скандал.
Ваша цель - написать программу, которая определила бы раз и навсегда такой порядок выступлений в Планетарном Совете, который гарантировал бы, что каждый член совета получает возможность высказаться раньше любого из своих потомков.
Ввод. В первой строке входного файла к этой задаче находится единственное число N, 1 ? N ? 100 - количество членов Марсианского Планетарного Совета. По многовековой традиции все члены Совета нумеруются натуральными числами от 1 до N. Далее во входном файле следуют ровно N строк, причем I-тая строка содержит список детей члена Совета с порядковым номером I. Список детей представляет собой последовательность порядковых номеров детей, разделенных пробелами и следующих в произвольном порядке. Список детей может быть пустым. Список детей (даже если он пуст) оканчивается нулем.
Вывод. Выходной файл должен в своей единственной строке содержать последовательность номеров выступающих, разделенных пробелами. Если несколько последовательностей удовлетворяют условиям задачи, то можно вывести любую из них.
Пример файла input.txt.
5 0 4 5 1 0 1 0 5 3 0 3 0Пример файла output.txt.
2 4 5 3 1Задача D. Пуговицы
фольклор, Л.Волков
Как уже несомненно стало известно всем, Екатеринбург добился права на проведение Летних Олимпийских игр 2032 года. Планируется, что России, как стране-организатору Олимпийских игр, будет разрешено внести минимальные изменения в программу Олимпиады. Так, с целью улучшения общего командного результата, было решено заменить соревнования по плаванию первенством в абсолютно новой игре "Пуговицы".
Правила игры очень просты. Перед двумя играющими находится кучка из K пуговиц. Играющие по очереди берут пуговицы из кучки, причем за один ход каждый из них может взять от 1 до L пуговиц. Выигрывает тот из спортсменов, которому удастся взять последнюю пуговицу.
Правила олимпийских соревнований будут лишь немного сложнее обычных. Тот из игроков, которому по жребию выпадает делать первый ход, получает возможность собственноручно назначить число K, руководствуясь в своем выборе только ограничениями 3 ? K ? 100,000,000 (именно столько пуговиц заготовлено для олимпийского турнира). Тот из игроков, который будет ходить вторым, выбирает, в свою очередь, число L, которое должно отвечать условию 2 ? L < K.
На вашу команду возлагается очень ответственная задание: необходимо написать программу, которая помогала бы второму игроку делать свой выбор. Другими словами, по заданному числу пуговиц в кучке K, необходимо определить такое число L, которое гарантирует победу второму игроку при наилучшей игре обеих сторон.
Так, например, если в кучке всего три пуговицы, то победу второму игроку обеспечивает выбор L=2. В самом деле, если первый игрок своим ходом заберет одну пуговицу, то второй сможет выиграть, взяв обе оставшихся пуговицы и, напротив, если первый возьмет две пуговицы, то второй победит, взяв последнюю.
Ввод. Входной файл для этой задачи состоит из одной строки, в которой записано единственное число K - количество пуговиц в кучке, выбранное первым игроком.
Вывод.
В выходной файл следует записать единственное целое число L - максимальное количество пуговиц, которое можно взять за один ход - обеспечивающее победу второму игроку. Если таких чисел несколько, то следует вывести наименьшее из них. Если таких чисел нет, то следует вывести число 0.
Пример файла input.txt. 3
Пример файла output.txt. 2
Задача E. Перестановки
Н.Шамгунов
Напомним, что перестановкой на некотором конечном множестве называется взаимно однозначное отображение этого множества на себя. Менее формально, перестановка - это способ переупорядочить элементы множества. Например, на множестве {1, 2, 3, 4, 5} можно задать перестановку
|
P(n) = ( |
1 | 2 | 3 | 4 | 5 | ) |
| 4 | 1 | 5 | 2 | 3 |
Такая запись определяет перестановку P следующим образом: P(1)=4, P(2)=1, P(3)=5 и т.д.
А чему равно значение выражения P(P(1))? Совершенно понятно - P(P(1))=P(4)=2. А, например, P(P(3))=P(5)=3. Легко понять, что если P(n) -перестановка, то и P(P(n)) тоже перестановка. В нашем примере (проверьте!)
|
P(P(n)) = ( |
1 | 2 | 3 | 4 | 5 | ) |
| 2 | 4 | 3 | 1 | 5 |
Естественно тогда обозначить эту перестановку так: P(P(n))=P2(n). Более общее определение выглядит так: P(n)=P1(n), Pk(n)=P(Pk-1(n)).
Среди всех перестановок особое положение занимает одна - та, которая ничего не переставляет:
|
EN(n) = ( |
1 | 2 | 3 | ... | N | ) |
| 1 | 2 | 3 | ... | N |
Совершенно понятно, что для любого k верно соотношение (EN)k=EN. Справедливо и менее тривиальное утверждение (мы не будем здесь его доказывать; решая задачу вы сами попутно получите доказательство): Пусть P(n) некоторая перестановка множества из N элементов. Тогда существует такое натуральное число k, что Pk=EN. Наименьшее натуральное k, такое, что Pk=EN, называется порядком перестановки P. Задача, которую должна решать программа, формулируется теперь очень просто: "дана перестановка, найти ее порядок".
Ввод. В первой строке входного файла записано единственное число N, удовлетворяющее двойному неравенству 1 <= N <= 1000 - количество элементов во множестве, на котором определена перестановка. Во второй строке, через пробел, записаны N различных натуральных чисел от 1 до N, задающих перестановку - числа P(1), P(2), ... , P(N).
Вывод. В выходной файл следует записать единственное натуральное число - порядок перестановки P. Можно считать, что ответ всегда не превосходит 109.
Пример файла input.txt #1.
5 4 1 5 2 3Пример файла output.txt #1.
6Пример файла input.txt #2.
8 1 2 3 4 5 6 7 8Пример файла output.txt #2.
1Задача F. Демократия в опасности
Л.Волков
В одном из островных государств Карибского бассейна все решения традиционно принимались простым большинством голосов на общем собрании граждан, которых, к счастью, было не очень много. Одна из местных партий, стремясь прийти к власти как можно более законным путем, смогла добиться некоторой реформы избирательной системы. Главным аргументом было то, что население острова в последнее время значительно возросло, и проведение общих собраний перестало быть легкой задачей.
Суть реформы состояла в следующем: с момента введения ее в действие все избиратели острова делились на K групп (необязательно равных по численности). Голосование по любому вопросу теперь следовало проводить отдельно в каждой группе, причем считалось, что группа высказывается "за", если "за" голосует более половины людей в этой группе, а в противном случае считалось, что группа высказывается "против". После проведения голосования в группах подсчитывалось количество групп, высказавшихся "за" и "против", и решение вопрос решался положительно в том и только том случае, когда групп, высказавшихся "за", оказывалось более половины общего количества групп.
Эта система вначале была с радостью принята жителями острова. Когда первые восторги рассеялись, очевидны стали, однако, некоторые недостатки новой системы. Оказалось, что сторонники партии, предложившей систему, смогли оказать некоторое влияние на формирование групп избирателей. Благодаря этому, они получили возможность проводить некоторые решения не обладая при этом реальным большинством голосов!
Пусть, например, на острове были сформированы три группы избирателей, численностью в 5, 5 и 7 человек соответственно. Тогда партии достаточно иметь трех сторонников в каждой из первых двух групп, и она сможет провести решение всего 6-ю голосами "за", вместо 9-и, необходимых при общем голосовании.
Вам надо написать программу, которая определяет по заданному разбиению избирателей на группы минимальное количество сторонников партии, достаточное, при некотором распределении их по группам, для принятия любого решения.
Ввод. Входной файл для этой задачи состоит из двух строк. В первой строке файла записано натуральное число K <= 101 - количество групп избирателей. Во второй строке через пробел записаны K натуральных чисел, которые задают количество избирателей в группах. Для упрощения определения понятия "большинство голосов" будем полагать, что и число групп, и количество избирателей в каждой группе суть нечетные числа. Вы можете также считать, что население острова не превосходит 10001 человек.
Вывод. В выходной файл следует записать единственное натуральное число - минимальное количество сторонников партии, способное решить исход голосования.
Пример файла input.txt.
3 5 7 5Пример файла output.txt.
6
Задача G. Вопросы и ответы
Л.Волков
База данных Пентагона хранит сверхсекретную информацию. Мы не знаем, что это за информация - она ведь сверхсекретная - зато знаем формат ее представления. Он удивительно прост. По неизвестным нам соображениям все данные кодируются натуральными числами от 1 до 5000. Размер основной базы (обозначим его через N) довольно велик - в ней может содержаться до 100000 таких чисел. База данных должна уметь быстро обрабатывать любые запросы, а самым распространенным из запросов является такой: "какой элемент является i-тым по величине", где i - натуральное число от 1 до N. Ваша программа должна выступить в роли диспетчера этой базы данных; другими словами она должна уметь быстро обрабатывать запросы описанного вида.
Ввод. Входной файл для этой задачи состоит из двух частей. Сначала в нем записана база данных, потом серия запросов к ней. Формат представления базы данных очень прост: в первой строке записано число N, затем в N следующих строках числа из этой базы по одному в строке и в произвольном порядке. Серия запросов записывается также просто: в первой строке этой серии записано количество запросов K, 1 <= K <= 100, и далее в K строках по одному в строке идут запросы. Запрос "какой элемент является i-тым по величине" записывается для краткости просто одним числом i. База данных отделяется от серии запросов строкой из трех решеток '#'.
Вывод. Выходной файл должен состоять из K строк, в каждой из этих строк должен быть записан ответ на соответствующий запрос. Ответом за запрос "i" является элемент из базы, который идет в ней i-тым по величине, считая с наименьшего. Пример файла input.txt.
5 7 121 123 7 121 ### 4 3 3 2 5Пример файла output.txt.
121 121 7 123Задача H. Снова D++
фольклор, Л.Волков, А.Лысенко
Язык D++, в развитие которого было вложено столько сил участниками наших мартовских соревнований, продолжает совершенствоваться. Его создатели пытаются сделать синтаксис языка как можно более простым и свободным с тем, чтобы облегчить программирование на этом языке будущего.
Конечно, некоторое минимальное количество правил должно остаться. Ваша программа должна проверять соблюдение некоторых из этих правил, связанных с расстановкой скобок и комментариями.
Текст правильной программы на D++ состоит из символьной части, арифметических выражений и комментариев. Комментарии могут встречаться где угодно и содержать любые символы. Комментарий всегда открывается парой символов '(*' и заканчивается парой символов '*)'. Каждый комментарий обязательно должен закрываться. Арифметические выражения в D++ всегда открываются круглой скобкой '(', закрываются круглой скобкой ')' и могут содержать внутри себя только символы '=+-*/0123456789)(' и, естественно, комментарии. Пробелы в арифметических выражениях не допускаются, однако разрешены переводы строк. Скобки в арифметическом выражении могут быть вложенными; при этом они обязаны быть сбалансированными. Это означает, кто как '((1)))', так и '(23))((+)' не являются правильными арифметическими выражениями. Правильность выражения определяется только правильностью расстановки в нем скобок.
Наконец, весь остальной текст программы (получающийся из исходного отбрасыванием всех комментариев и арифметических выражений) может состоять из произвольных символов, за исключением символов '(' и ')'.
Ввод. Во входном файле записан некоторый текст. Объем этого текста не превышает 10000 символов. В тексте могут встречаться латинские буквы, цифры, скобки, знаки арифметических действий и символы конца строки и возврата каретки.
Вывод. В выходной файл программа должна записать YES, если введенный текст является корректной программой на D++ и NO в противном случае. Пример файла input.txt #1.
Hello, here is a sample D++ program. It contains some arithmetical expressions like (2+2=4), (2+-/*) and ((3+3)*3=20(*this is not true, but you don't have to verify it :-) *)+8) (* the closing bracket in the previous comment is also in order, since this bracket does not belong to any arithmetical expression*)Пример файла output.txt #1.
YESПример файла input.txt #2.
(*) In this file, a comment is opened, but never closed.Пример файла output.txt #2.
NO