||🏠
||Чемпионат Урала
||Четвертьфинал ICPC
||УрКОП
||Все соревнования
||Фото
||История
||Новичкам ||
Задачи и решения районного тура
XLII-ая ОБЛАСТНАЯ МАТЕМАТИЧЕСКАЯ
ОЛИМПИАДА ШКОЛЬНИКОВ
2001 - 2002 учебный год
Задачи и решения районного тура (7-11 классы)
Составители:
С.Э.Нохрин, Е.Г.Пыткеев, В.Т.Шевалдин, С.Н.Васильев (ИММ УрО РАН).
7 класс
7.1. Верно ли, что 8 натуральных чисел 1,2,3,4,5,6,7,8 можно разбить на две группы по 4 числа в каждой так, чтобы сумма чисел в первой группе равнялась сумме чисел во второй группе и сумма квадратов чисел во первой группе равнялась сумме квадратов чисел во второй группе?
Решение. Сумма чисел от 1 до 8 равна 36, а сумма их квадратов - 204. Следовательно, нужно найти четверку чисел из 1,...,8, сумма чисел которой равна 18, а сумма квадратов - 102. Считаем, что эта четверка содержит 8. Тогда сумма квадратов остальных трех чисел четверки равна 38. Это влечет, что в четверке нет 7 и 6, а есть 5, т.к. 12+22+32+42 £ 38. Тогда сумма двух оставшихся чисел равна 18-(8+5) = 5, а сумма их квадратов равна 102-(64+25) = 13. Это однозначно определяет пару чисел 2,3.
Ответ. {2,3,5,8}, {1,4,6,7}.
7.2. На плоскости отметили 6 различных точек. Известно, что прямая, проходящая через любые две из этих точек, содержит по крайней мере еще одну отмеченную точку. Докажите, что все отмеченные точки лежат на одной прямой.
Решение. Пусть отмечены точки A1, A2, ... A6. Рассмотрим прямую, проходящую через точки A1 и A2. По условию на ней есть еще отмеченная точка; без ограничения общности можно считать, что это точка A3. Предположим, что рассматриваемая прямая не содержит какой-либо из отмеченных точек, скажем, не содержит точку A6. Тогда на прямых A1A6, A2A6 и A3A6 есть еще по крайней мере по отмеченной точке (кроме точек A1, A2, A3 и A6). Однако, на самом деле, таких точек не более двух (это A4 и A5). Полученное противоречие показывает, что предположение о том, что прямая A1A2 содержит не все отмеченные точки, ошибочно.
7.3. Сравните два трехзначных числа [ ` abc] и [ ` bad], если верны два неравенства: [ ` ac] > [ ` bd] и [ ` bc] > [ ` ad]. (Среди цифр a, b, c и d могут быть равные).
Решение. Из условия [ ` ac] > [ ` bd] следует, что либо a > b, либо a = b и c > d. В первом случае [ ` ad] > [ ` bc] вопреки условию. Остается случай a = b и c > d (в котором оба данных неравенства, очевидно, верны). Но тогда у чисел [ ` abc] и [ ` bad] цифры сотен равны, цифры десятков равны, а цифра единиц больше у первого.
Ответ. [ ` abc] > [ ` bad].
7.4. Фокусник спрятал под одну из 8 положенных в ряд шапок монету. Как за три попытки узнать, под какой шапкой она лежит, если Вы можете показывать на шапку (попытка), а фокусник, если Вы не угадали, говорит, слева или справа от указанной Вами шапки находится монета? При этом фокусник два раза подряд не говорит правду и два раза подряд не врет.
Решение. Укажем на крайнюю слева шапку. Если там монета, то мы её обнаружили за одну попытку. Если её там нет, то она лежит правее и по ответу фокусника мы будем знать, солгал он или нет, а потому будем знать, правду или ложь он скажет после второй (а также и после третьей) попытки. Итак, после первой попытки у нас осталось семь шапок и мы точно знаем, как понимать слова фокусника. Второй попыткой выберем среднюю из семи оставшихся шапок, если монеты под ней нет, то по ответу фокусника определяется группа из трех шапок, содержащая монету. Укажем на среднюю из этих трех шапок. Если монеты там нет, то по ответу фокусника мы будем точно знать, под какой из двух оставшихся шапок лежит монета.
8 класс
8.1. Папа у Васи силен в математике, но по дороге в гараж забыл код цифрового замка у гаража. В памяти у папы осталось, что все цифры кода различны и их сумма равна 28. Сколько различных кодов нужно перебрать папе, чтобы наверняка открыть гараж, если открывающий механизм замка состоит из четырех дисков с полным набором цифр на каждом?
Решение. Среди цифр кода есть 9 и 8. Иначе, поскольку все цифры кода различны, наибольшая сумма цифр кода не превзойдет 9+7+6+5. Тогда остальные две цифры кода £ 7 и их сумма равна 11. Возможны два варианта: {7,4} и {6,5}. Подсчитаем число возможных кодов. Цифра 9 может занять любое из 4 мест. Тогда для 8 останутся три возможности. Итак, различных вариантов расположения 9 и 8 будет 4·3 = 12. Два оставшихся места должны занять либо 7 и 4, либо 5 и 6, причем для каждой пары имеется два варианта. Следовательно, число возможных кодов составляет 12·4 = 48.
Ответ. 48.
8.2. В банке летают 3 мухи. Всякий раз, когда мухи со скодостями A > 0 и B > 0 сталкиваются, они разлетаются со скоростями [(A2+2AB)/( A+B)] и [(B2)/( A+B)]. Может ли через некоторое время оказаться, что все мухи удвоили свои скорости? (От столкновения до столкновения муха летает с постоянной скоростью, одновременно 3 мухи столкнуться не могут).
Ответ. Все мухи одновременно удвоить свои скорости не могут.
Решение. Заметим, что после столкновения мух со скоростями A и B сумма их первых скоростей составит
|
8.3. Треугольник \triangleABC прямоугольный, AB - его гипотенуза. На прямой AB по обе стороны от гипотенузы вне ее отложены отрезки AK = AC и BM = BC. Найдите угол Ð KCM.
Ответ. 1350.
Решение. Треугольники \triangleAKC и \triangleBMC равнобедренные. Отсюда, и по теореме о внешнем угле треугольника получаем:
|
|
8.4. Докажите неравенство
|
Решение. Нужно сложить 4 однотипных легко проверяемых неравенства:
|
9 класс
9.1. На бобину, имеющую форму цилиндра высоты H и радиуса основания R, равномерно в один слой намотана тонкая проволока, образующая K полных витков (K - натуральное число). Концы проволоки лежат на разных основаниях цилиндра, а прямая, их соединяющая, параллельна оси цилиндра. Найдите длину проволоки.
Ответ. Ö {H2+4 p 2R2K2}.
Решение. Разрежем боковую поверхность бобины по прямой, соединяющей концы проволоки, и развернем ее на плоскость (см. рисунок).
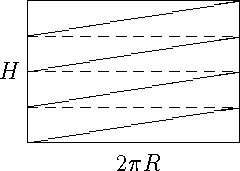
|
9.2. Хоккейный матч "Нью-Джерси Дэвилс" - "Колорадо" закончился со счетом 8:5 в пользу "Дьяволов" из Нью-Джерси. Докажите, что в матче был момент, когда команде "Нью-Джерси Дэвилс" оставалось забить столько шайб, сколько команда "Колорадо" забила к этому времени.
Решение. Пусть x - разность между количеством шайб, оставшихся забить команде из Нью-Джерси, и количеством шайб, забитых "Колорадо" на данный момент. В начале матча x = 8, а в конце x = -5. При каждой шайбе, забитой любой из команд, число x уменьшается на 1. Следовательно, был момент, число x было равно 0, т.е. когда количество шайб, которые осталось забить "Нью-Джерси Дэвилс", равнялось количеству шайб, забитых на данный момент командой из Колорадо.
Замечание. Идея решения называется дискретной непрерывностью.
9.3. Стороны прямоугольника выражаются целыми числами. Какой длины они должны быть, чтобы периметр прямоугольника численно равнялся площади?
Ответ. ( 4 ; 4 ) или ( 3 ; 6 ).
Решение. Пусть a и b - длины сторон прямоугольника. Тогда 2(a+b) = ab. Это равенство равносильно следующему: (a-2)(b-2) = 4. В последнем равенстве либо оба сомножителя равны 2, либо один из них равен 1, а другой 4. Поэтому получаем два ответа: ( 4 ; 4 ) и ( 3 ; 6 ).
9.4. По крайней мере одно из чисел a, b, c или d отлично от нуля. Доказать неравенство
|
Решение. Неравенство равносильно следующему:
|
|
10 класс
10.1. Пусть sin a +sin b = 1. Найдите наименьшее и наибольшее значения выражения cos a +cos b .
Ответ. max(cos a +cos b ) = Ö 3, min(cos a +cos b ) = - Ö 3.
Решение. Пусть cos a +cos b = t. Тогда
|
10.2. Пусть S - фигура на плоскости XOY, состоящая мз всех точек, координаты которых удовлетворяют двойному неравенству x2 £ y £ 9. Докажите, что площадь этой фигуры больше 35.
Решение. В дугу параболы y = x2 (-3 £ x £ 3) впишем ломаную с вершинами A(-3,9), B((-2,4), C(-1,1), O(0,0), D(1,1), E(2,4), F(3,9). Плоская фигура ABCODEF состоит из двух трапеций и одного треугольника. Ясно, что площадь этой фигуры меньше площади фигуры S из условия задачи. При этом легко подсчитать, что площадь многоугольника ABCODEF (сумма площадей трапеций AFEB, BEDC и треугольника CDO) равна (6+4)/2·5+(4+2)/2·3+2·1/2 = 35.
10.3. В вазе лежит N конфет (N - натуральное число). Аня, Володя и Витя играют в "жадину" по следующим правиилам: они по очереди (сначала Аня, затем Володя, затем Витя, снова Аня и т.д.) берут из вазы и тут же съедают несколько конфет, причем Аня берет не менее одной и не более трех конфет, а каждый из мальчиков - не менее одной и не более двух конфет. Съевший последнюю конфету из вазы объявляется жадиной. При каких натуральных N Витя и Володя, действуя согласованно, могут оставить "жадиной" Аню, как бы та ни сопротивлялась этому?
Ответ. При N = 5k+1, k = 0,1,2 ¼
Решение. Если N = 5k+1, то стратегия мальчиков такова: если Аня берет три конфеты, оба мальчика берут по одной, если Аня берет две, то один из мальчиков возьмет одну конфету, а второй две, наконец, если Аня берет одну конфету, то каждый из мальчиков должен взять по две. В итоге за три взятия число конфет уменьшится ровно на 5, и через k таких циклов Аня будет вынуждена съесть последнюю конфету из вазы.
Если N ¹ 5k+1, то Аня первым же ходом добъется того, что число конфет в вазе будет либо 5k+1, либо 5k+2. Дальше ей следует каждый раз брать конфеты так, чтобы чтобы число конфет, взятых ею и мальчиками за последнее последнее взятие, было равно 5. Легко проверить, что это возможно. В конце конце концов после очередного хода Ани в вазе останутся одна или две конфеты, и один из мальчиков должен будет стать "жадиной".
Замечание. Описанная стратегия мальчиков в случае N = 5k+1 - единственная, приводящая к выигрышу. Напротив, стратегия Ани в случае N ¹ 5k+1 - не единственно возможная выигрышная. Например, если перед ходами мальчиков в вазе лежало 12 конфет, а мальчики взяли по две, то Аня может взять как две конфеты, так и одну. Ей только необходимо следить за тем, чтобы после ее хода оставшееся число конфет при делении на 5 давало остаток 1 или 2.
10.4. Докажите, что для любого целого числа n ³ 0 существует натуральное число m такое, что число 1\underbrace00...03n+21\underbrace99...9m делится на 1\underbrace00...0n1.
Решение. Имеем
|
|
|
11 класс
11.1. Существуют ли пять последовательных натуральных чисел, сумма квадратов которых есть квадрат целого числа?
Решение. Заметим, что
|
11.2. Дан правильный шестиугольник ABCDEF. На его диагоналях BF и FD выбраны точки M и N соответственно так, что
|
Решение. Пусть сторона шестиугольника равна a. Заметим, что Ð FAB = Ð AFE = 1200 и Ð ABF = Ð BAF = Ð DFE = Ð FDE = 300. Так как треугольник \triangleFAB равнобедренный, то FB = 2 FA cos300 = 2a [( Ö 3)/ 2] = Ö 3a. Тогда и FD = FB = Ö 3a. Отсюда BM = [BF/( Ö 3)] = a и FN = [FD/( Ö 3)] = a. Для доказательства того, что точки A, M, N лежат на одной прямой, достаточно доказать, что Ð FAN = Ð FAM. Треугольники \triangleAFN и \triangleABM - равнобедренные, т.к. AB = BM = AF = FN = a. Тогда Ð MAB = (1800- Ð ABM)/2 = (1800-300)/2 = 750. Следовательно, Ð FAM = Ð FAB - Ð MAB = 1200-750 = 450. Заметим, что Ð DFA = Ð AFE = - Ð EFD = 1200-300 = 900 . Так как треугольник \triangleNFA - прямоугольный и равнобедренный, то Ð FAN = 450. Итак, углы Ð FAN и Ð FAM равны, и этим все доказано.
11.3. Числа a, b, c, d положительны. Докажите неравенство
|
Решение. Перепишем правую часть неравенства в виде 4(a-b+b-c+c-d). Легко проверяются неравенства
|
11.4. В некотором государстве, в котором всего 10 городов, сеть железных дорог устроена следующим образом: все города стоят на кольце; кроме того, один из городов (столица) соединен отдельными ветками со всеми остальными городами (кроме соседей по кольцу). Сеть разбита на участки. Каждый участок - это кусок железной дороги между какими-то городами, не проходящий через другой город. Правительство постановило разделить эти участки между двумя компаниями так, чтобы из любого города в любой другой можно было проехать как по дорогам первой компании, так и по дорогам второй. Можно ли выполнить то постановление?
Ответ. Нельзя.
Решение. Количество участков в сети 17 (десять на кольце и еще семь дорог из столицы). Согласно принципу Дирихле одной из компаний будет принадлежать не более 8 участков. Предположим, что по дорогам этой компании можно проехать из любого города в любой другой. Тогда граф, вершинами которого являются города, а ребрами - участки дорог, принадлежащие этой компании, связен. Но в этом графе число вершин v = 10, а число ребер r £ 8, в то время как в связном графе должно выполняться неравенство r ³ v-1. Следовательно, предположение неверно.
Примечание. Граф называется связным, если для любых двух его вершин v1 и vn существует последовательность вершин v2, v3, ... vn-1 таких, что вершины vi и vi+1 (i = 1,2,... n-1) соединены ребром.
Составители:
С.Э.Нохрин, Е.Г.Пыткеев, В.Т.Шевалдин, С.Н.Васильев (ИММ УрО РАН).
File translated from TE X by TT H, version 2.25.
On 17 Dec 2001, 23:06.