||🏠
||Чемпионат Урала
||Четвертьфинал ICPC
||УрКОП
||Все соревнования
||Фото
||История
||Новичкам ||
Система подготовки олимпиадных задач по программированию в УрГУ
Алексей Самсонов, Александр Ипатов
В статье описан процесс подготовки задач для олимпиад по программированию, проходящих в Уральском государственном университете (Екатеринбург). Рассматриваются учебно-методологические аспекты отбора задач, организация коллективной работы над задачами, используемые компьютерные инструменты. Приводятся рекомендации для членов жюри олимпиад по программированию.
1. Введение
Олимпиады по программированию пользуются большой популярностью в России. В полуфинале командного студенческого чемпионата мира по программированию ACM ICPC ([1]) ежегодно участвуют сотни команд. Для школьников проводятся Всероссийская олимпиада по информатике ([2]) и Всероссийская командная олимпиада по программированию ([3]). Кроме того, регулярно проходит множество Интернет-соревнований ([4], [5]), на которых участники могут оттачивать свои навыки решения алгоритмических задач, программирования и работы в команде.
Для организации любого из этих соревнований жюри должно подготовить комплект задач (на командных соревнованиях среднее количество задач — 10). Задачи должны быть оригинальными, их сложность должна соответствовать уровню участников, при этом они должны быть подготовлены качественно и не должны содержать ошибок. К сожалению, из-за роста сложности олимпиадных задач и потребности в них, ошибки жюри на различных соревнованиях в последние годы стали нормой. Некоторые грубые ошибки (например, неверные решения жюри или тесты) приводят к несправедливым результатам соревнований, другие (опечатки в условии) не столь критичны. Однако все ошибки в задачах вызывают негативную реакцию участников соревнований и ведут к падению престижа как конкретного соревнования, так и всего олимпиадного движения в целом.
В России разработано множество вспомогательных инструментов для облегчения и автоматизации работы жюри. Так, для написания программ, проверяющих вывод участников, стандартом стала библиотека TestLib, разработанная в СПбГУ ИТМО и Саратовском ГУ ([6]). Однако более сложные компьютерные системы, предназначенные для подготовки задач, такие как библиотека скриптов СПбГУ ИТМО или проект Polygon ([7]), не заслужили общего признания. Эти системы автоматизируют рутинные процессы (например, проверку решения жюри на всех подготовленных тестах), но не страхуют от глубоких методических ошибок при подготовке задач.
Уральский государственный университет проводит региональные соревнования по программированию с 1997 года. В последнее время университет организует шесть крупных соревнований в год ([8]): личное и командное первенство УрГУ, четвертьфинал студенческого чемпионата мира, чемпионат Урала, личную и командную олимпиаду среди школьников Свердловской области. Программный комитет УрГУ ежегодно готовит около 60 олимпиадных задач по программированию. Для обобщения опыта подготовки комплектов и улучшения их качества была разработана система подготовки задач, которая кратко описывается в этой статье. Следует уделить внимание тому, что под «системой» мы подразумеваем не столько компьютерную систему и программное обеспечение, сколько методы организации коллективной работы над задачами и набор методических рекомендаций, связанных с различными этапами подготовки комплекта задач. По умолчанию, наши рекомендации относятся к командным соревнованиям с онлайн-проверкой, хотя большинство из них может быть применено и к любым другим олимпиадам по программированию.
2. Программный комитет
Под программным комитетом соревнований по программированию в УрГУ мы понимаем группу людей, ответственных за подготовку комплектов олимпиадных задач. В их обязанности входит поддержка банка идей задач, проработка идей задач и составление строгих формулировок, формирование комплекта задач для конкретных соревнований, а также непосредственно подготовка задач: составление условий, разработка системы тестов, авторских решений, программ проверки корректности входных данных (валидаторов), программ проверки ответов участников (чекеров).
Программный комитет состоит из 10-15 человек. Большая часть членов программного комитета являются старшекурсниками, аспирантами или недавними выпускниками УрГУ, которые в прошлом активно участвовали в соревнованиях по программированию, а сейчас работают в университете или занимаются промышленной разработкой программного обеспечения. Работа в программном комитете ведётся на некоммерческой основе, в свободное от основной работы время. Состав программного комитета постоянно обновляется — некоторые члены комитета теряют желание или возможность тратить своё личное время на подготовку задач, в то же время комитет пополняется более молодыми членами, закончившими свои выступления в официальных соревнованиях.
Все члены программного комитета имеют большой опыт участия в соревнованиях, при этом многие добивались значительных результатов (так, восемь членов текущего программного комитета выходили в финал чемпионата мира по программированию ACM ICPC). Благодаря этому, программный комитет хорошо разбирается в олимпиадных задачах и может грамотно оценивать их сложность. Также ему известны современные тенденции в олимпиадном движении (популярные темы для задач, появление новых инструментов для их подготовки). Знакомство с технологиями промышленной разработки позволяет комитету использовать при подготовке задач удобное программное обеспечение и методы организации коллективной работы.
3. Формирование комплекта задач
3.1. Банк идей задач
Программный комитет поддерживает банк идей задач, из которого формируется большая часть комплектов для соревнований, проводимых в УрГУ. В банк заносятся идеи задач из общей рассылки олимпиадного сообщества УрГУ, куда помимо программного комитета входят некоторые преподаватели факультета, бывшие участники соревнований и прочие заинтересованные люди. Любой желающий может предложить возникшую у него идею задачи любой степени готовности — это может быть уже продуманная и сформулированная олимпиадная задача, интересный факт или алгоритм, на использование которого предлагается сделать задачу, любопытная модель какого-либо процесса из реальной жизни, и так далее. В качестве источников вдохновения обычно выступают: окружающая действительность, научная деятельность, другие олимпиадные задачи.
Идея помещается в один из разделов банка: «готовые задачи», «нерешённые задачи» и «не продуманные / не сформулированные задачи». После того как удаётся превратить идею задачи в строгое математическое условие или найти её решение в некоторых ограничениях, эта идея может перейти в другой раздел банка. Срок хранения идеи в банке неограничен, и процесс формулирования задачи и поиска решения может продолжаться достаточно долго. Так, осенью 2010 года программный комитет доработал и включил в очередной комплект сразу две идеи, впервые предложенные около десяти лет назад.
Главным преимуществом банка идей является централизованная схема сбора идей и гарантия того, что все предложенные задачи не потеряются и с большой вероятностью будут использованы в будущем. Важно отметить, что подписчики рассылки стараются предлагать «оригинальные» и необычные идеи задач, поскольку задачи на простое использование стандартных методов или алгоритмов для них не очень интересны. Впрочем, как будет отмечено ниже, такие задачи иногда добавляются программным комитетом в комплект искусственно.
3.2. Отбор задач из банка идей
Когда определяются сроки и состав участников очередного соревнования, программный комитет собирается для формирования комплекта задач. Большая часть задач выбирается из раздела «готовые задачи» банка идей. Главные факторы, влияющие на выбор задач — статус соревнования (отборочный этап, открытый фестиваль) и уровень его участников. Программный комитет старается составить чёткое представление о знаниях и опыте участников, чтобы для каждой задачи примерно оценить, сколько команд будут способны её решить и сколько времени им на это понадобится. Для каждой задачи формулируется её функциональная роль в комплекте. Например, «утешительная задача, которую должны решить все команды». Или, «самая сложная задача, на которую лидеры, решившие все остальные задачи комплекта, должны потрать много времени». Или, «задача на построение конструкции, для решения которой в команде должен быть сильный математик». Окончательная формулировка задачи (ограничения, наличие или отсутствие дополнительных трудностей в реализации, крайних случаев) выбирается исходя из предполагаемой функциональной роли. Таким образом, задачи подстраиваются под комплект, в котором они будут использованы. На этом же этапе программному комитету может понадобиться придумать дополнительные задачи для комплекта, под заданную функциональную роль. В качестве примеров таких задач может выступать очень простая задача с запоминающейся или шуточной формулировкой или стандартная задача на технику программирования, которая может занять одного из членов команды, пока другие участники будут решать другие, идейно более сложные задачи.
Программный комитет должен представлять себе итоговую таблицу результатов — именно она служит наилучшим показателем успешности подбора задач на соревнование. Если несколько команд решили все предложенные задачи или, напротив, многие команды не смогли решить ничего, это свидетельствует о неадекватной оценке сложности комплекта. Нужно также стараться минимизировать количество задач, которые решили все команды, и количество задач, которые не решил никто — эти задачи не «разделяют» команды и бесполезны со спортивной точки зрения. В пользу комплекта обычно говорят плавное (а не скачкообразное) возрастание количества решённых задач при движении по таблице результатов снизу вверх и плавный рост сложности задач. Вторую величину можно оценивать так: упорядочить задачи по количеству команд, которые их решили, после чего проверить, что отношение количества команд для любых соседних по сложности задач не должно быть слишком велико (желательно, чтобы оно не превосходило двух). Если соревнование является отборочным, и лучшие команды по его итогам попадают в следующий этап, то полезно также стараться максимизировать время выхода — количество минут, которое потратила команда из нижней части «выходящей зоны», чтобы решить такое количество задач, которое обеспечило ей выход в следующий этап. Классическим примером неудачной оценки времени выхода является ситуация, когда слабая команда на старте соревнования решает две-три простых задачи, не может за оставшееся время решить ни одну из других задач (поскольку они существенно сложнее), но выходит в следующий этап, благодаря малому штрафному времени. Самый простой способ увеличения времени выхода — добавление задач с простой идеей решения, но с «подводными камнями» или трудностями в реализации, на преодоление которых команды могут потратить много времени.
4. Процесс подготовки комплекта
Подготовка комплекта задач воспринимается как программный проект с жёсткими сроками сдачи и малым временем на реализацию (от двух недель до двух месяцев). Программный комитет выделяет людей, входящих в активную команду разработчиков (от четырёх до восьми человек), и назначает одного из разработчиков менеджером разработки. Команда разработчиков одновременно работает над всеми задачами комплекта. Менеджер контролирует ход подготовки комплекта (в частности, он в курсе текущей ситуации с подготовкой каждой задачи) и указывает разработчикам на вопросы, которые нужно решить в первую очередь. Кроме того, по каждой задаче назначаются ответственный и рецензент. Ответственный за задачу должен разработать систему тестов, написать правильные и неправильные решения жюри, валидатор (программу проверки корректности входных данных) и чекер (программу проверки ответов участников). Рецензент пишет альтернативное решение задачи, исследует и дополняет набор тестов, проверяет корректность валидатора и чекера. При этом все остальные члены команды разработчиков также должны быть в курсе ситуации по задаче, проверять чужие решения, валидаторы и чекеры на наличие ошибок и по возможности добавлять свои решения. Условия задач пишутся разработчиками либо по собственному желанию, либо по указанию менеджера. Для некоторых действий по подготовке задачи применяется аутсорсинг — передача их членам программного комитета, не входящим в команду разработчиков, или другим желающим. Обычно на аутсорсинг отдаётся подготовка особого класса тестов для задачи или перевод условия задачи на английский язык.
Главный инструмент совместной работы над комплектом задач — система контроля версий, в частности — Subversion. Репозиторий (хранилище данных) с общим доступом решает проблему синхронизации данных на разных компьютерах. Кроме того, в системе контроля версий хранятся все предыдущие версии файлов, что позволяет легко отменять и отслеживать внесённые изменения.
Системы контроля версий активно используются при подготовке олимпиад в России и в мире в качестве удобного общего хранилища информации. Однако в УрГУ роль Subversion существенно важнее. В команде разработчиков принято при внесении изменений в какой-либо файл описывать все эти изменения в поле «Комментарий». В результате журнал (лог-файл) внесённых изменений содержит всю информацию о том, на каком этапе находится подготовка каждой задачи и какую проблему решает каждый разработчик (см. рис. 1). Чтение лог-файла позволяет хорошо ориентироваться в текущем состоянии комплекта и является рекомендуемым для всех разработчиков. При этом менеджер обязан читать все записи в журнале, чтобы контролировать ход работы, а ответственный и рецензент должны читать все записи по своей задаче.
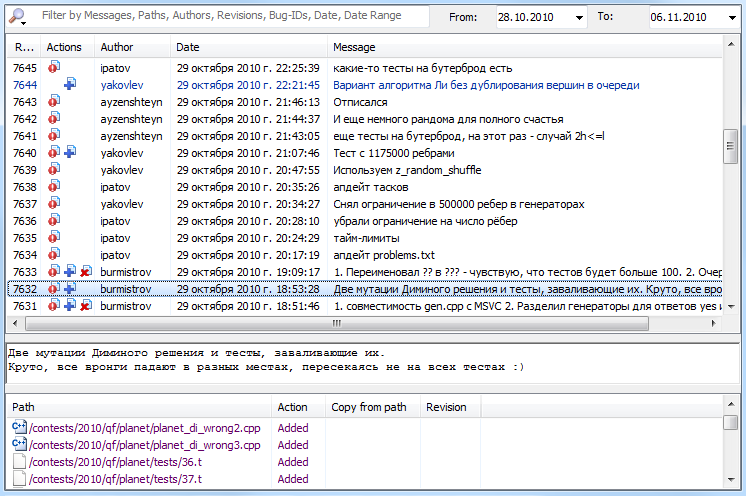
Рис. 1. Пример журнала внесённых изменений — для каждого изменения указан его автор, время, список изменённых файлов и комментарий, оставленный разработчиком.
Другой полезной функцией, которой обладает, например, клиент TortoiseSVN ([9]), является удобный интерфейс сравнения различных версий одного и того же файла (см. рис. 2). Он не только позволяет подробнее ознакомиться с изменениями, которые внёс в файл разработчик, но и существенно облегчает процесс рецензирования этих изменений. После синхронизации с сервером каждый разработчик просматривает внесённые в интересующие его файлы правки и проверяет, что они действительно оправданы, устраняют какую-либо проблему, а главное — что они не содержат ошибок. Рецензия чужого кода позволяет значительно понизить вероятность ошибок при подготовке задач, поскольку один и тот же код проверяют несколько человек.
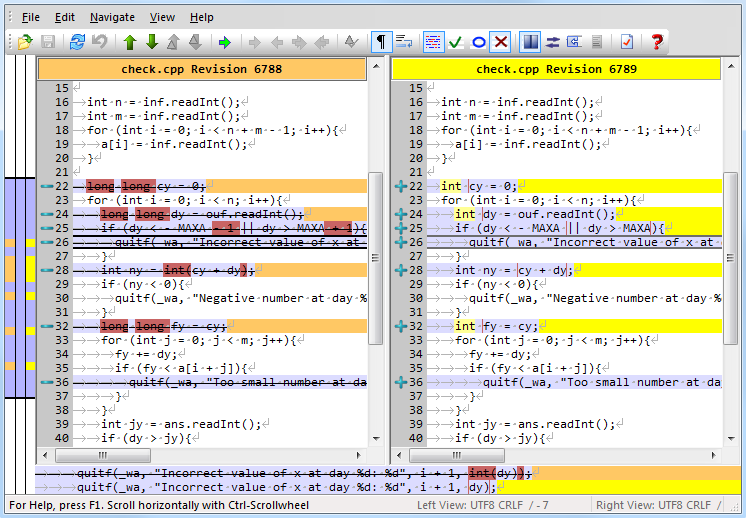
Рис. 2. Сравнение текущей версии файла check.cpp с его предыдущей версией. Был изменён тип данных некоторых переменных (с long long на int), а также изменены ограничения на область допустимых значений переменной dy (строка 25).
Утилита сравнения различных версий файла и рецензирование также активно используются при подготовке условий — разъяснении непонятных моментов, избавлении от неоднозначности трактовки, исправлении стилистических, орфографических и пунктуационных ошибок. Подробнее процесс подготовки условий описан в пункте 5.2.
Менеджер также может использовать систему контроля версий для организации коллективной разработки — достаточно просто записывать в файл, лежащий в общем репозитории, ответственных и рецензентов, наиболее приоритетные действия по подготовке задач, текущую информацию о подготовке комплекта.
Также несомненным плюсом системы контроля версий является возможность работать без доступа к Интернету, только иногда подключаясь к Сети для синхронизации данных. Каждый разработчик использует свой собственный компьютер и удобный для него набор инструментов: операционную систему, файловые менеджеры, среды разработки, компиляторы, и добавляет результат своей работы в репозиторий в ранее оговоренном формате. Работа напрямую с файловой системой обычно отнимает у разработчика меньше времени, чем использование каких-либо сложных программ или веб-сервисов.
Итак, использование системы контроля версий позволяет синхронизировать данные на разных компьютерах, при необходимости возвращаться к более ранним версиям, управлять коллективной разработкой, следить за ходом подготовки комплекта, рецензировать чужую работу и вовремя находить в ней ошибки. При этом каждый разработчик может пользоваться удобным для него инструментарием, придерживаясь лишь договорённостей о формате организации файлов.
5. Подготовка задачи
Процесс подготовки каждой задачи комплекта можно разбить на следующие этапы: придумывание легенды (идеи для развёрнутого условия задачи), написание и вычитывание этого условия, подготовка правильных, неверных и неэффективных решений задачи, написание чекеров и валидаторов, разработка системы тестов. Остановимся на каждом из этих действий подробнее.
5.1. Легенда
Большая часть идей, хранящихся в банке, сформулированы на строгом математическом языке и в терминах той области, к которой относится решение задачи (теория графов, теория чисел, строковые алгоритмы и т. д.). В то же время, на многих соревнованиях, в том числе и в УрГУ, принято писать для задач развёрнутые условия, зачастую оперирующие не математическими терминами, а общими понятиями. Программный комитет считает важным оценивать умение участников грамотно строить математическую модель по такому «литературному» условию. Таким образом, программный комитет вынужден «моделировать наоборот» — придумывать «жизненные» ситуации, которые будут сводиться к отобранным на соревнование задачам из банка идей. Часто в результате этого процесса задачи существенно усложняются, поскольку участники могут так и не перейти от условия к подразумевавшейся исходно (достаточно простой) задаче.
Рассмотрим пример составления легенды. Возьмём следующую задачу:
Дан ориентированный граф, его
вершины занумерованы числами от 1 до n. За одну операцию разрешается поменять
местами номера любой пары вершин. Требуется найти последовательность операций,
после выполнения которой все дуги будут вести из вершин с меньшим номером в
вершины с большим номером, или указать, что это невозможно.
Задача не представляет трудностей для опытного участника соревнований по программированию. Достаточно найти любой порядок топологической сортировки графа (стандартным алгоритмом), после чего из исходной перестановки вершин получить требуемую перестановку с помощью транспозиций. Как сформулировать эту задачу без использования терминов из теории графов? Один из способов — представить вершины как города, а дуги — как односторонние дороги и придумать, как задать операцию обмена номеров вершин. Вместо этого можно перейти к совсем другим объектам — матрицам. Если мы рассмотрим матрицу смежности графа, то операция обмена номеров двух вершин с номерами i и j соответствует последовательному обмену строк и столбцов с номерами i и j. Вершины графа занумерованы в порядке топологической сортировки в том и только в том случае, если его матрица смежности верхнетреугольная. Программный комитет предложил на Открытый чемпионат УрГУ 2010 года следующую задачу (приведена сокращённая формулировка, полный текст условия можно найти на сайте [10], задача 1781).
В n аудиториях пройдёт n
мероприятий. Составлена таблица из нулей и единиц размером n × n,
в которой в i-й строке и j-м столбце стоит единица, если i-я аудитория
задействована в проведении j-го мероприятия. После первого мероприятия должна
быть свободна первая аудитория, после второго — первая и вторая, и т. д.
За одну операцию разрешается выбрать два числа i и j, поменять местами i-ю и
j-ю строку, а потом — i-й и j-й столбец. Выдайте последовательность
операций, после проведения которой описанное условие будет выполняться.
Основная сложность этой задачи заключается в грамотной формализации описанной операции и переходе от матриц к графам, а написание решения не представляет труда. Однако, во время интернет-соревнования, проходившего по задачам этого чемпионата, с задачей справились лишь 5 из 467 участников со всего мира, и она стала самой сложной задачей комплекта.
5.2. Условие
Условие задачи пишется по продуманной идее легенды (см. предыдущий пункт) и состоит из следующих частей: описание задачи, описание формата входных и выходных данных, примеры. В условии указываются ограничения на входные данные и способ рассмотрения крайних случаев (при их наличии). В некотором смысле, ошибки в условиях являются самыми критичными. В отличие от тестов и решений жюри, которые хранятся только на компьютерах жюри, условия раздаются всем участникам. Следовательно, от ошибок в условии страдают все участники соревнований. Наконец, если условие можно трактовать несколькими способами, команды ставятся в неравное положение — команды, понявшие задачу не так, как её авторы, не имеют возможности правильно решить её, и зачастую факты подобного непонимания обнаруживаются только после завершения соревнований.
Программный комитет УрГУ уделяет много внимания подготовке условий — после появления первой версии условие рецензируется многими разработчиками. В среднем каждое условие проходит через 7-8 версий. Иногда изменения являются лишь небольшими стилистическими правками, а иногда (например, если легенда признаётся неудачной) условие полностью переписывается. Файл с условием задачи хранится в системе контроля версий. Все условия готовятся в формате LATeX с использованием стандартного в России стилевого файла для оформления задач olymp.sty, разработанного жюри олимпиад в Санкт-Петербурге. Поскольку формат LATeX (в отличие от формата MS Word) является текстовым, все изменения, вносимые в условия, легко отслеживать с помощью утилиты сравнения файлов разных версий (см. пункт 4). Программный комитет уделяет большое внимание типографским деталям и единообразному оформлению задач (например, по умолчанию во всех задачах для использования переменных используются строчные латинские буквы).
При определении формата входных и выходных данных, а часто и ограничений, следует в первую очередь руководствоваться легендой, и уже затем – удобством подготовки задачи или простотой написания решений. Следует помнить о «неявных» ограничениях, которые могут следовать из условия задачи. Например, если в условии сказано, что x — количество яблок, то уравнение x + a = 5 не имеет решений при a = 6, поскольку количество не может быть отрицательным.
Рассмотрим пример условия олимпиадной задачи и укажем на ошибки и неточности в нём:
Вася хотел написать на бумажке
n последовательных натуральных чисел в порядке неубывания, но, пока он это
делал, он отвлёкся и одно из чисел пропустил. Ещё не поздно ему помочь —
восстановите пропущенное число.
Формат ввода. В первой строке записано число n (1 ≤ n ≤ 1000000), а во второй строке записаны числа a1, a2, ..., an − 1, которые Вася записал на бумажке (1 ≤ ai ≤ 100000).
Формат вывода. Выведите число, которое забыл написать Вася. Если однозначно определить это число нельзя, выведите «IMPOSSIBLE».
Пример
| Входные данные | Вывод |
|
4 2 3 5 6 |
4 |
Несмотря на то, что условие короткое и простое, в нём много ошибок, неточностей и неудачных решений. Начнём с мелких замечаний. Во-первых, лучше отказаться от использования термина «натуральные числа», потому что, в зависимости от системы определений, они включают или не включают ноль. Во-вторых, «неубывание» следует заменить на «возрастание», поскольку последовательные числа различны. Лучше убрать обозначения для чисел, записанных Васей, поскольку они не используются нигде, кроме формата входных данных. При этом индексы использованы неудачно (из обозначений можно подумать, что числа, которые хотел написать Вася – это a1, a2, ..., an, а значит, во входных данных не указано только последнее из этих чисел).
У задачи есть и более серьёзные проблемы. Так, в примере к задаче содержится ошибка (входные данные не удовлетворяют описанному формату). Фраза «нельзя определить однозначно» означает, что есть ноль или не менее двух способов. Но в условии не сказано, что Вася может ошибаться в тех числах, которые он написал. А значит, из условия неясно, нужно ли участнику обрабатывать случай, когда задача не имеет ни одного решения. Целесообразно разделить формат вывода для двух принципиально разных случаев: «ответа нет» и «ответ неоднозначен». Во втором случае можно просить выдать слово «AMBIGUITY» вместо «IMPOSSIBLE». Можно решить проблему и другим способом, попросив выдать любой из правильных ответов и написав чекер, проверяющий корректность ответа в случае его неоднозначности.
Если предположить, что Вася может ошибаться, то, формально, он может писать и нецелые числа, так как обратное не указано в формате входных данных. Хотя, здесь возможна и другая трактовка (ведь в задаче речь идёт только о целых числах, а нецелые числа вообще не упоминаются). Если n = 1, то во второй строке не записано ни одного числа. В этом случае задача практически не имеет смысла, в качестве ответа может выступать любое целое положительное число, а значит, участник вправе выдать верный ответ длиной в два миллиона цифр (ограничения на ai указаны в формате входных данных, а значит, не обязательно соответствуют ограничениям на числа, которые Вася хотел написать), и разработчикам придётся позаботиться о том, чтобы такой ответ был принят. Наконец, в текущей версии ограничение сверху на n в 10 раз больше ограничения на числа во второй строке, а значит, при больших n задача никогда не будет иметь решения. Если же мы увеличим ограничение на числа, записанные Васей, до миллиона, то максимальный размер файла со входными данными будет составлять примерно 7 мегабайт. Если размер тестов будет велик, это может замедлить проверку решений, что особенно критично в случае интернет-соревнования с сотнями участников, которые быстро напишут и отправят на проверку решение этой простой задачи и создадут длинную очередь проверки. Поскольку столь высокие ограничения в данной задаче не принципиальны, их можно уменьшить в 10 раз.
Итак, приведём пример исправленного условия задачи.
Вася хотел написать на бумажке n последовательных
целых положительных чисел в порядке возрастания, но, пока он
это делал, он отвлёкся и одно из чисел пропустил. Ещё не поздно ему помочь —
восстановите пропущенное число.
Формат ввода. В первой строке записано целое число n (2 ≤ n ≤ 105). Во второй строке содержится n − 1 число, записанное Васей. Все эти числа целые, положительные и не превосходят 105.
Формат вывода. Если Вася гарантированно ошибся, и не существует ни одного способа восстановить пропущенное число, выведите «IMPOSSIBLE». В противном случае выведите число, которое забыл написать Вася. Если существует несколько вариантов ответа, выведите любой.
Примеры
| Входные данные | Вывод |
|
5 2 3 5 6 |
4 |
|
3 2 5 |
IMPOSSIBLE |
5.3. Авторские решения
Ответственный и рецензент должны подготовить по своей задаче набор различных решений: правильных, неверных и неэффективных. Желательно написать хотя бы одно верное решение на языке Java или C#, поскольку часто решения, написанные на этих языках, работают медленнее их точных аналогов на Pascal или C++, что следует учитывать при выставлении ограничений по времени. В задачах, где есть простое, но асимптотически медленное решение, и сложное эффективное решение, которое необходимо придумать и реализовать участникам, программный комитет должен определиться, решения с какой асимптотической сложностью должны засчитываться как «верные», а с какой — нет. Например, все решения не хуже O(n2∙log(n)) должны засчитываться, а все решения за O(n3) — нет. Следует реализовать верное решение и асимптотически медленное решение, ускоренное с помощью неасимптотических оптимизаций. Ограничения на размер входных данных следует подбирать таким образом, чтобы неэффективное решение работало дольше эффективного не менее чем в 8-10 раз. При этом ограничение по времени должно превышать время работы верного решения на максимальном тесте в 2-3 раза.
Отдельное внимание следует уделить формально неверным решениям, которые, однако, могут находить правильный ответ для большинства входных данных. Это могут быть решения, использующие жадный алгоритм в задачах, где он на самом деле не применим, а также решения, использующие различные эвристики и численные методы. Во многих задачах хороший результат дают случайные алгоритмы. Команда разработчиков должна реализовать такие решения и проверить, что они не проходят некоторые из подготовленных тестов. Подробнее о методике составления тестов см. пункт 5.5.
Как уже отмечалось выше, система контроля версий позволяет разработчикам использовать в подготовке авторских решений любые среды программирования и компиляторы — в репозиторий добавляется лишь исходный текст программы, который просматривается и рецензируется другими членами команды разработчиков. Для автоматизированной проверки решений на наборе тестов (количество которых может достигать нескольких сотен) используется разработанная в УрГУ утилита «Тестер» ([11]). Помимо проверки того, что решение выдаёт правильный ответ на все тесты, она позволяет автоматически генерировать ответы к тестам на основе эталонного решения, измерять время работы программы и объём использованной памяти.
5.4. Чекеры
Чекеры необходимы в тех ситуациях, когда ответ на задачу для некоторых входных данных неоднозначен. В частности, чекеры активно используются в задачах, где помимо ответа нужно выдать сертификат — информацию, по которой легко убедиться в корректности такого ответа. Например, в задаче на поиск минимума функции ответом служит искомый минимум, а сертификатом — аргумент функции, при котором этот минимум достигается; в задаче на поиск кратчайшего расстояния между двумя вершинами графа ответом служит длина кратчайшего пути между вершинами, а сертификатом — сам этот путь. Иногда требование выдачи сертификата усложняет решение задачи. Однако это требование позволяет подготовить задачу надёжнее и сделать процесс подготовки более удобным: с помощью чекера можно удостовериться в том, что авторское решение находит корректный (но не обязательно оптимальный) ответ; в противном случае, чекер выдаёт информацию о том, где именно в ответе содержится ошибка, что позволяет быстрее обнаружить ошибку в эталонном решении. Наконец, в случае расхождения ответов на тест у жюри и участников, по сертификату участников чекер может удостовериться, что их ответ неверен, либо «поднять тревогу», сообщив жюри о том, что эталонное решение жюри не является правильным.
Из предыдущего абзаца следует, что чекер должен быть способен определять, что ответ участников «лучше» ответа жюри. Для примера рассмотрим, как должен выглядеть чекер для задачи о поиске кратчайшего пути между двумя вершинами в графе:
- Если ни участник, ни жюри не нашли путь, то ответ участника правильный. Если участник не нашёл путь, а жюри нашло его, то ответ участника неверный.
- Если участник нашёл путь, то чекер проверяет, что это действительно корректный путь от стартовой до конечной вершины, а его длина равна длине, указанной участником. После этого возможны три исхода: если длина пути жюри меньше длины пути участника, то ответ участника неверный (найден не кратчайший путь); если длина пути жюри больше длины пути участника или жюри вообще не нашло путь, то ответ жюри неверный; если же длины путей у жюри и участника совпадают, то ответ участника правильный.
Обратите внимание, что хотя чекер не решает задачу самостоятельно, за счёт сертификата он может проверить, какой из двух ответов лучше. Также стоит отметить, что чекер не проверяет сертификат в ответе жюри. Действительно, если авторское решение выдаёт некорректный ответ на какой-либо тест, то при проверке этого решения чекер выдаст вердикт «неправильный ответ», даже если ответ, выданный авторским решением, будет в точности совпадать с ответом в наборе тестов!
Для разработки чекеров программный комитет использует библиотеку Testlib для языка C++, созданную в Саратовском ГУ ([6]). Использование этой библиотеки облегчает процесс синтаксического анализа файла с ответом участника. Скажем, функция чтения целого числа из файла автоматически проверяет, что это число в файле действительно есть и что оно попадает в область допустимых значений стандартного 32-битного целочисленного типа данных.
5.5. Тесты
Процесс подготовки тестов к любой задаче начинается с создания валидатора — программы, проверяющей корректность входных данных. Валидатор проверяет, что формат файла со входными данными в точности соответствует описанному в условии: везде в файле стоит нужное количество пробелов и переводов строк, в конце файла нет лишней информации, все данные удовлетворяют указанным ограничениям. В валидаторах иногда проверяются и более сложные ограничения — например, связность заданного в файле графа или отсутствие общих точек у двух геометрических фигур. Для удобного синтаксического анализа файла со входными данными в валидаторах используется либо библиотека Testlib, либо разработанная специально для этих целей в УрГУ библиотека Strict.h [12].
Ответственный за задачу старается разработать максимально полный набор тестов. Он должен включать множество небольших тестов на разные случаи, ответы на которые легко проверить вручную, тесты на крайние случаи (в том числе, с минимально и максимально возможными входными данными), большие тесты, сгенерированные по какому-либо шаблону, а также достаточное количество случайных тестов разного размера. Также следует убедиться в том, что асимптотически медленные, эвристические и случайные решения (см. пункт 5.3) не проходят какие-либо из подготовленных тестов. Для этого нужно либо специально готовить тесты против таких решений, либо воспользоваться техникой стресс-тестирования. Для проведения стресс-тестирования пишется генератор случайных тестов и чекер. Далее генерируется случайный тест, на нём запускаются два решения (обычно — эталонное и неверное), полученные ответы сравниваются. Если ответы расходятся, то тест против неверного решения готов. Если же ответы совпадают, генерируется новый случайный тест, и так до тех пор, пока не обнаружится расхождение. Стресс-тестирование позволяет находить неочевидные тесты против эвристик, увеличивает надёжность подготовки задачи: если в задаче требуется выдать сертификат, можно запускать стресс-тестирование эталонного решения и проверять, что оно пройдёт все сгенерированные тесты. Интересной техникой подготовки тестов является стресс-тестирование эталонных решений с малыми изменениями (например, стресс-тестирование эталонного решения, в котором допущена небольшая ошибка, например, одно из строгих неравенств заменено нестрогим). Это позволяет быстро строить сложные тесты на крайние случаи и лучше исследовать задачу (иногда такие «малые изменения» в действительности не влияют на корректность решения, что может быть на первый взгляд неочевидно).
Для уменьшения сетевого трафика и размера архива с материалами соревнования в систему контроля версий вместо больших тестов (размер которых может достигать нескольких мегабайт) добавляются программы, генерирующие эти тесты, а сборка полной версии тестового набора осуществляется с помощью скриптов. Важно заметить, что генераторы случайных тестов должны работать детерминированно — создавать один и тот же тест, вне зависимости от времени запуска и используемого компилятора (это не относится к генераторам, используемым при стресс-тестировании). Для этого можно, например, реализовать свой генератор псевдослучайных чисел для языка C++ или использовать язык со стандартизированным генератором чисел (например, Java). Теперь для того, чтобы заново сгенерировать некоторый большой тест, достаточно передать генератору псевдослучайных чисел ту же самую затравку (seed).
6. Обучение и преемственность
Программный комитет соревнований в УрГУ постоянно пополняется новыми членами. В связи с этим были предприняты меры для быстрого обучения работе в программном комитете: написаны наборы рекомендаций по созданию тестов, чекеров, валидаторов, авторских решений и условий. Кроме того, подготовлен наглядный пример «правильно» подготовленной задачи, демонстрирующий принятый формат организации файлов при работе с системой контроля версий. Этот пример содержит: готовое условие в формате LATeX, примеры валидатора и чекера, написанные с использованием библиотек Testlib и Strict.h, пример конфигурационного файла для Тестера, позволяющий быстро проверять на подготовленных тестах, авторские решения, примеры генераторов, использующие детерминированный генератор псевдослучайных чисел, наконец, пример скрипта, компилирующего генератор и создающего с его помощью полный набор тестов к задаче.
Значительную роль в обеспечении преемственности играют олимпиады для школьников Свердловской области. По традиции задачи для школьников готовят студенты младших курсов, ещё участвующие в студенческих соревнованиях. Они полностью осуществляют всю разработку комплекта — от сбора идей задач до их подготовки и проведения самого соревнования. Так они учатся использовать технологии и методы организации работы программного комитета УрГУ. При этом их работа контролируется и рецензируется членами «основного» программного комитета.
7. Заключение
За прошедшие годы в УрГУ была создана стабильная и продуманная система подготовки задач, которая позволяет каждый год готовить комплекты для шести различных очных соревнований. Организован процесс обучения подготовке задач, обеспечена преемственность. Так, последние школьные олимпиады готовились практически по той же самой системе, хотя в разработке задач не принимал участия ни один из создателей этой системы. Комплекты задач соревнований в УрГУ заслуживают положительные отзывы участников, претензии по качеству условий крайне редки. О качестве тестов свидетельствует тот факт, что в 60 подготовленных за 2009/2010 учебный год задачах на данный момент не найдено ни одной ошибки в тестах и чекерах.
Система подготовки олимпиадных задач достаточно гибкая и постепенно изменяется с течением времени — программный комитет пробует использовать новые вспомогательные инструменты и методы организации работы. В настоящий момент ведётся работа над улучшением вспомогательных инструментов (библиотек), автоматизацией некоторых рутинных процессов. Обдумывается возможность использования в разработке гибкой методологии (Agile), систем отслеживания ошибок (багтрекеров). Также обсуждаются способы уменьшения количества времени, которое тратится на подготовку задач, при незначительном снижении её качества.